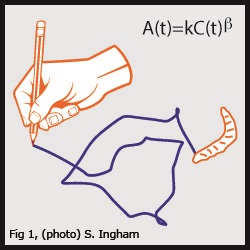
The speed – curvature power law in Drosophila larval locomotion

When we scribble our name on a piece of paper, the speed of the pen is related to the curvature of the path by means of a power law. Namely, our slowing down upon snakier lines is scale invariant: the precise speed-curvature relationship is maintained regardless of how fast or slow the movement is. We found that the trajectories traced by fly larvae, while crawling searching for food, also comply with such power law. Thus, a basic principle of human motor control may be at work in the humble maggot, amenable to neuro-mechanical dissections and with a much smaller brain.

Original abstract:
We report the discovery that the locomotor trajectories of Drosophila larvae follow the power-law relationship between speed and curvature previously found in the movements of human and non-human primates. Using high-resolution behavioural tracking in controlled but naturalistic sensory environments, we tested the law in maggots tracing different trajectory types, from reaching-like movements to scribbles. For most but not all flies, we found that the law holds robustly, with an exponent close to third-fourth rather than to the usual two-third found in almost all human situations, suggesting dynamic effects adding on purely kinematic constraints. There are different hypotheses for the origin of the law in primates, one invoking cortical computations, another viscoelastic muscle properties coupled with central pattern generators. Our findings are consistent with the latter view and demonstrate that the law is possible in animals with nervous systems orders of magnitude simpler than in primates. Scaling laws might exist because natural selection favours processes that remain behaviourally efficient across a wide range of neural and body architectures in distantly related species.